I have stumbled upon a slight issue in solving one of the Paper 4's, could someone please explain how to go about solving this ?
part (d) & (e) of question 5, on the attached sheet.
Ok here goes the (d) part.
Let midpoint of the chord be G,perpendicular from centre bisects the chord AC.
Now AG = 1.8 m
Now two right angled triangles AOF and AGE are similar, therefore their corresponding sides will be proportional
OA/AG= AF/GE
2/1.8=5/GE
GE=(5*1.8)/2 = 4.5 m
CHeck the attached image.
e) Consider the triangle OGC. OG =
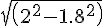)
= 0.87
Let the point where GE intersects the circle be M.
MG = 2 + 0.87 = 2.87
Thus ME = 4.5 - 2.87 = 1.63
OE = ME + OM = 3.63
OD =
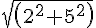)
=
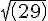)
Consider the right angled triangle ODE. OE = 3.63, OD =
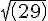)
, thus
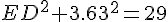
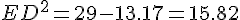
ED =
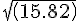)
= 3.97
FE = ED = 3.97
FD = 8 (app.)
Area of trapezium = 0.5* (3.6+8)*4.5 = 26.1
Area of whole Shape = 26.1 + Area of the semi-circle ABC.
Area of semi-circle ABC = 2.913
Thus the area of the whole shape = 29cm^2