Indeed it its! Could you please show how you got it?
I took out a factor of 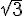 , but could never get the answer!
, but could never get the answer!
OK....i'll elaborate.
I'll simplify the numbers first.
(,/3)
-3 + (,/3)
-2 + (,/3)
-1 + (,/3)
0 + (,/3)
1 + (,/3)
2 + (,/3)
3Now we can simplify : Anything to the power of zero is 1 and a square root to the power of 2 results in the number being squared
(,/3)
-3 +
3-1 + (,/3) +
1 + (,/3) +
3 + (,/3)
3Now we add the numbers only.
1 + 3 + 1/3 + (,/3)
-3 + (,/3)
-1 + (,/3)
1 + (,/3)
3Anything to the power of negative factor can be written as 1 over the value
Example : x
-1 ----> 1/x
Hence => 13/3 + 1/(,/3)
3 + 1/(,/3) + (,/3) + (,/3)
3Now you need to rationalise, that is multiply by (,/3)/(,/3) so that you obtained all the roots in the numerator. Moreover (,/3)
2 = 3 ---> (,/3)
3 = 3(,/3)
13/3 + (,/3)/9 + (,/3)/3 + (,/3) + 3(,/3)
Now forget about the (,/3) and add its coefficients to get the required solution
 13/3 + 40(,/3)/9
13/3 + 40(,/3)/9Hope it helps
