(a) For a triangle ABC, show that
(i) AB is perpendicular to BC
(ii) BM = CM, where M is the midpoint of AC
(b) Find also an equation of circle passing through A, B & C
okay, i can help in a)i) part
for AB to be perpendicular to BC, the product of their gradients shud be -1
lets try, 'm' of AB = (9-3)/(5-1) = 6/4 = 3/2
'm' of BC = (7-9)(8-5) = -2/3
3/2 * -2/3 = -1
hence proved.
a)ii) first find the co-ordinates of M i.e ((8+1)/2, (7+3)/2) = (4.5,5)
length of BM =
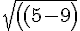^2 + (4.5-5)^2)
=
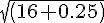)
=
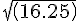)
= 4.03
length of CM=
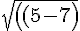^2 + (4.5-8)^2)
=
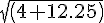)
=
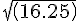)
= 4.03
b) Eqn of a circle = (x-h)^2 + (y-k)^2 = r^2
h,k = co-ordinates of the center of the circle, here of M
h = 4.5
k = 5
r = 4.03
(x-4.5)^2 + (y-5)^2 = 16.25
Hence proved
@Dude - SOrry i cudnt help much, i used my add. math knowledge to solve this for him. U have a lotta Qs to solve..
