Thanks for your help guys, this question is still bothering me though. Whoever can solve this is a genius! I can't believe this question was from C1.
The equation of a curve is
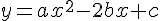
, where
a,
b and
c are constants with
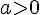
.
a) Find, in terms of
a,
b and
c, the coordinates of the vertex of the curve.
b) Given that the vertex of the curve lies on the line
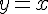
, find an expression for
c in terms of
a and
b. Show that in this case, whatever the value of
b,
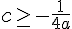
.
I've partially answered the question (I've done parts a) and a bit of b), but don't know how to show that the statement in b) is correct).
Here are my answers so far:
a)
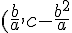)
b)
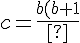}{a})
, but I don't know how to 'show that...'.
Many many thanks in advance!