. let a1,a2,a3,...be a sequence defined by
a1=1,an=3an-1; n?1
Show that an=3^n-1 for all positive integers n.
Prove the following statement.
n
2. ? 1/(2i-1)(2i+1)=n/2n+1 for each positive integer n.
1
3. Use mathematical induction to prove that (5^n)+(9^n)+2 is divisible by 4,for n?Z+.
Thanks.
1.
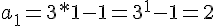
SO p(1) is true. Suppose p(k) is true, prove p(k+1) trues
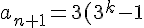 -1=3*3^k-3-1=3^{k+1} -4)
Are you sure this question is right?
2.
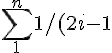(2i+1) =1/2 \sum_1^n 1/(2i-1) -1/(2i+1)=1-1/(2n+1)=1/2(2n/(2n+1))=n/(2n+1))
3.p(1) 5+9+2=16 hence p(1) is true
suppoose p(k) is true then (5^k)+(9^k)+2 is divisible by 4
p(k+1)-p(k) (5^(k+1))+(9^(k+1))+2-(5^k)-(9^n)-2 =5^k(5-1) +9^k(9-1)=4*5^k +8*9^k which is divisible by 4