Ok I'll put forward a general induction argument. This is going to be a long post. I have an IB HL book which lists out five steps involved in an induction proof. They are:
1. Prove the result for an initial value usually (n = 1).
2. Assume the result is true for another value n = k, k>1 stating the result.
3. Consider the case n = k + 1, writing down the goal clearly - the required form.
4. Using the assumption, now show that the result is true for n = k + 1.
5. Communicate why this proves this result using mathematical induction.
There are some comments at the end of the proof.
Our conjecture is

where

Write it as:
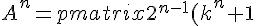 & 2^{n-1}(k^n - 1)\\ 2^{n-1}(k^n - 1) & 2^{n-1}(k^n + 1) \end{pmatrix} ) Step 1:
Step 1: when n = 1.
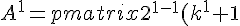 & 2^{1-1}(k^1 - 1)\\ 2^{1-1}(k^1 - 1) & 2^{1-1}(k^1 + 1) \end{pmatrix} = \begin{pmatrix} (k + 1) & (k - 1)\\ (k - 1) & (k + 1) \end{pmatrix} )
which is clearly true since A raised to 1 is A itself.
Step 2: So lets assume for some integer j, the formula is true. Notice we're not using n = k here (as described in the five steps above) as we already have a variable k.
 Step 3:
Step 3: Substitute n = j + 1 in the original equation.
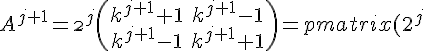(k^{j+1} + 1) & (2^{j})(k^{j+1} - 1)\\ (2^{j})(k^{j+1} - 1) & (2^{j})(k^{j+1} + 1) \end{pmatrix})
This is what we have to prove, using the assumption in Step 2.
Step 4: The ugly calculations!
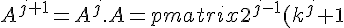 & 2^{j-1}(k^j - 1)\\ 2^{j-1}(k^j - 1) & 2^{j-1}(k^j + 1) \end{pmatrix} . \begin{pmatrix} (k + 1) & (k - 1)\\ (k - 1) & (k + 1) \end{pmatrix}<br />= \begin{pmatrix} (k + 1)(k^j + 1)(2^{j-1}) + (k - 1)(k^j - 1)(2^{j-1}) & (k - 1)(k^j + 1)(2^{j-1}) + (k + 1)(k^j - 1)(2^{j - 1}) \\ (k - 1)(k^j + 1)(2^{j-1}) + (k + 1)(k^j - 1)(2^{j - 1}) & (k + 1)(k^j + 1)(2^{j-1}) + (k - 1)(k^j - 1)(2^{j-1}) \end{pmatrix}<br />= \begin{pmatrix} 2^{j-1}(k^{j+1} + k^j + k + 1 + k^{j+1} - k^j - k + 1) & 2^{j-1}(k^{j+1} - k^j + k - 1 + k^{j+1} - k + k^j - 1) \\ 2^{j-1}(k^{j+1} - k^j + k - 1 + k^{j+1} - k + k^j - 1) & 2^{j-1}(k^{j+1} + k^j + k + 1 + k^{j+1} - k^j - k + 1) \end{pmatrix}<br />= \begin{pmatrix} 2^{j-1}(2(k^{j+1} + 1)) & 2^{j-1}(2(k^{j+1} - 1)) \\ 2^{j-1}(2(k^{j+1} - 1)) & 2^{j-1}(2(k^{j+1} + 1)) \end{pmatrix}<br />= \begin{pmatrix} (2^{j})(k^{j+1} + 1) & (2^{j})(k^{j+1} - 1)\\ (2^{j})(k^{j+1} - 1) & (2^{j})(k^{j+1} + 1) \end{pmatrix} ) Step 5:
Step 5: Conclude that this matrix is same as the one that appeared at the end of step 3. So the result is true for n = j + 1 when true for n = j. Since it is true for n = 1, it is true

by the principle of Mathematical Induction.
Since the project is being judged for presentation, notation and whatnot. I strongly recommend that your friend sticks to the notation I used, (as they are straight out of an IB (HL) book

) and lays out her proof in an organized manner.
