hey guys  ,
,
i have more doubts from the O/N 2008 paper 1.
its Q5, how do we relate maximum/minimum values to the given function?
is it from graph or something?
and Q10 (ii), i don't know how to prove max. value of gf(x)=9.
Can someone help me step by step?
For question 5:(i)The maximum value of the curve will occur when it is
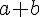
, and thus in this case the value is 10.
The minimum value will occur when it is
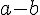
, and thus the value is
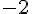
. We have to remember that both
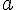
and
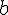
are positive constants. The actual value of
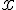
does not matter in this question.
(ii)
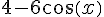=0)
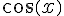=\frac{2}{3})
I got,
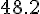
and
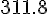
degrees
(iii) Should look something like a hill, with to intersections with the x axis in the positive region or the first quadrant.
For question 10:This is simple,
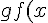=-9x^2+30x-16)
Thus simply differentiate it to get the point at which the value is the maximum,
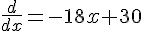
And the value that you get for
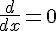
is
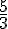
If you put this value of x to the formula for
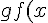)
, then you get 9.
Hope this helped.