« previous next »
Pages: 1 ... 28 29 [30] 31 32 ... 37   Go Down

Author Topic: [CIE] All Pure Mathematics (P1, P2 and P3) doubts here !  (Read 85428 times)

Offline astarmathsandphysics

  • SF Overlord
  • *********
  • Posts: 11271
  • Reputation: 65534
  • Gender: Male
  • Free the exam papers!
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #435 on: October 10, 2011, 09:53:28 pm »
And does  hg mean h times g or h(g)
Logged

Offline astarmathsandphysics

  • SF Overlord
  • *********
  • Posts: 11271
  • Reputation: 65534
  • Gender: Male
  • Free the exam papers!
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #436 on: October 10, 2011, 09:55:39 pm »
It mean h(g)
f=x^2 -4x+7=(x+2)^2 +3
take h=g^2 +3 and g=x-2
« Last Edit: October 10, 2011, 10:03:06 pm by astarmathsandphysics »
Logged

Offline Sea Lover

  • SF Citizen
  • ***
  • Posts: 131
  • Reputation: 375
  • Gender: Female
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #437 on: October 10, 2011, 10:00:26 pm »
I'm sorry ,made a mistake while copying the question is like this:
The function f is defined by
f(x) = x^2 - 4x + 7 for x > 2.
The function g is defined by
g(x) = x - 2 for x > 2.
The function h is such that f = hg and the domain of h is x > 0.
(iii) Obtain an expression for h(x).

Logged

Offline astarmathsandphysics

  • SF Overlord
  • *********
  • Posts: 11271
  • Reputation: 65534
  • Gender: Male
  • Free the exam papers!
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #438 on: October 10, 2011, 10:03:36 pm »
My post is amended.
Logged

Offline Sea Lover

  • SF Citizen
  • ***
  • Posts: 131
  • Reputation: 375
  • Gender: Female
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #439 on: October 10, 2011, 10:05:21 pm »
and no the answer in the mark scheme wasn't like this, I just don't know how it came?
Logged

Offline Sea Lover

  • SF Citizen
  • ***
  • Posts: 131
  • Reputation: 375
  • Gender: Female
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #440 on: October 10, 2011, 10:06:30 pm »
can you please explain it further
Logged

Offline Sea Lover

  • SF Citizen
  • ***
  • Posts: 131
  • Reputation: 375
  • Gender: Female
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #441 on: October 10, 2011, 10:08:59 pm »
no thanx I got it , thanx so much
Logged

Offline astarmathsandphysics

  • SF Overlord
  • *********
  • Posts: 11271
  • Reputation: 65534
  • Gender: Male
  • Free the exam papers!
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #442 on: October 10, 2011, 10:09:31 pm »
In fact that is not the ponly possible answer. What about g=x^2 -4x and h=g+7?
There are any number of possible answers.
Logged

Offline ashwinkandel

  • SF Citizen
  • ***
  • Posts: 144
  • Reputation: 521
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #443 on: October 11, 2011, 05:09:30 am »
@Sea Lover I have attached the solution
Logged

Offline ashwinkandel

  • SF Citizen
  • ***
  • Posts: 144
  • Reputation: 521
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #444 on: October 11, 2011, 08:23:58 am »
Urgent Help Needed Got board exams tomorrow. I have attached the question here:
Logged

Offline astarmathsandphysics

  • SF Overlord
  • *********
  • Posts: 11271
  • Reputation: 65534
  • Gender: Male
  • Free the exam papers!
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #445 on: October 11, 2011, 09:10:02 am »
f : x  ? 3 ? 2 tan(1 x)
should that be tan^-1 x
Logged

Offline Arthur Bon Zavi

  • |Sun of Tomorrow... =]|
  • SF V.I.P
  • ********
  • Posts: 5849
  • Reputation: 65041
  • Gender: Male
  • Fiducia in questo uomo ciecamente.
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #446 on: October 11, 2011, 09:26:52 am »
(7) (i)

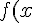First keep the value of x as 0 in f(x), you will get 3. Then keep a higher value, for example f(0.5 pie), you will get 1. So as you move from 0 to pie, the value of f(x) is decreasing so the range is : f(x)\le3

(ii)

f(2/3 pie)
= 3 - 2tan(0.5 X 2/3 pie)
= 3 - 2tan(1/3 pie)
= 3 - 2 (\sqrt3)
= \sqrt3(\sqrt3 - 2)

(iii)

You simply need to draw the graph. Make sure you plot the graph only for the range given in the question.

(iv)

f(x) = 3 - 2 tan(\frac{1}{2}x), then let f(x) be y

y = 3 - 2tan((\frac{1}{2})x)
2tan(\frac{1}{2}x) = 3 - y
tan(\frac{1}{2}x) = \left(\frac{3-y}{2} \right)
\frac{1}{2}x = tan-1\left(\frac{3-y}{2} \right)
x = 2 X tan-1\left(\frac{3-y}{2} \right)

y = 2 X tan-1\left(\frac{3-y}{2} \right)
« Last Edit: October 11, 2011, 09:40:41 am by Arthur Bon Zavi »
Logged

Continuous efforts matter more than the outcome.
- NU

Offline astarmathsandphysics

  • SF Overlord
  • *********
  • Posts: 11271
  • Reputation: 65534
  • Gender: Male
  • Free the exam papers!
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #447 on: October 11, 2011, 09:35:14 am »
thanks
Logged

Offline Arthur Bon Zavi

  • |Sun of Tomorrow... =]|
  • SF V.I.P
  • ********
  • Posts: 5849
  • Reputation: 65041
  • Gender: Male
  • Fiducia in questo uomo ciecamente.
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #448 on: October 11, 2011, 09:41:15 am »
Logged

Continuous efforts matter more than the outcome.
- NU

Offline ashwinkandel

  • SF Citizen
  • ***
  • Posts: 144
  • Reputation: 521
Re: All Pure Mathematics DOUBTS HERE!!!
« Reply #449 on: October 11, 2011, 10:16:28 am »
@Arthur Bon Zavi If you can , can you plz show me show the graph looks like?? This is the first time i have come through a question in CIE Maths exam where graph of tanx has been asked to plot... I know how to plot for y=tanx ... but this y=3-tan(x/2)  for domain 0<=x<2pi seems complicated..
Logged
Pages: 1 ... 28 29 [30] 31 32 ... 37   Go Up
« previous next »