Question : Suggest a possible equation for each of the graphs.
here
http://img707.imageshack.us/img707/103/scan0001cn.jpg
http://img197.imageshack.us/img197/4797/byhbyh.jpg
plz explain the steps to solve them too.
thanks
I love the names you give to your images man! Keep up the good work!

(e)
(x+2)(x))
The line passes through two negative points and the origin.
(f)
(x-1)(x-2))
The left side of the curve is going downward. This means that it is a negative curve. There are two interceptions where the x-axis is positive. Therefore two (x-z)s.
(g)
^2(x-3))
The left side is negative, so it the curve is negative. It has a standing point with 2 interceptions on the x-axis, so there is a
)
somewhere. And it cuts the x-axis in the positive area. Thus, it has an (x-z).
(h)
)
There is a stationary point on (0,0) meaning that there is
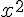
and there is an intersection on the negative part of the x-axis. So, there is a (x+z).
(i) Although this may seem intimidating, it is actually based on the simple rules as previous.
(x+2)(x+1)(x-3)(x-2)(x-1))
You can see that there are 6 straight line sections. So the total power of
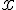
with be

.
Now, there are 3 intersections in the positive and the negative, so you will have a repeated brackets of these:
)
and
)
Now, determining the the slope is very important. Before you do such big ones, just plot them in your head. Now even powers e.g
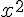
will always have their negative x values on the positive y-axis. So,

is no exception. But the graph we see shows that the negative x values are on the negative y-axis.
So, we put in a negative sign, and problem solved!
