lol....Now I finally know how to use the latex thingy...cool
ohk...check the pic to look how the tangents are
We next find the acute angle, between the two tangents.
The equation of the curve is
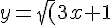)
i.e
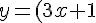^(1/2))
differentiating with respect to x
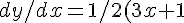^(-1/2) (3))
so
![dy/dx= 3/2 [1/ \sqrt(3x+1)]](https://studentforums.biz/cgi-bin/mimetex.cgi?dy/dx= 3/2 [1/ \sqrt(3x+1)])
we know
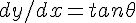
Gradient of tangent at P
![dy/dx= dy/dx| (0,1)= 3/2[ 1/\sqrt(3(0) +1)]=3/2](https://studentforums.biz/cgi-bin/mimetex.cgi?dy/dx= dy/dx| (0,1)= 3/2[ 1/\sqrt(3(0) +1)]=3/2)
If the angle made by the tangent with the +ve direction of x axis is
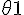
then
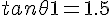
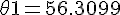
Gradient of tangent at Q is given by
![dy/dx|q= dy/dx|(1,2)= 3/2[ 1/\sqrt(3(1)+1)]=3/4](https://studentforums.biz/cgi-bin/mimetex.cgi?dy/dx|q= dy/dx|(1,2)= 3/2[ 1/\sqrt(3(1)+1)]=3/4)
If the angle made by the tangent with the +ve direction of x axis is
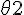
then
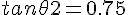
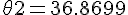
Let the tangent to the curve at point P intersect the x axis at point S and the tangent at point Q intersect the x axis at the point T.
Let the two tangents intersect at the point R.
Consider
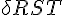
In
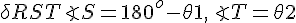
Now
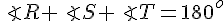
so
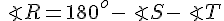
i.e
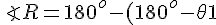- \theta 2 = \theta 1 - \theta 2)
so angle between the tangents =
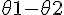
== 56.3099° – 36.8699° = 19.44°
I feel so good to help....that satisfaction
