« previous next »
Pages: [1]   Go Down

Author Topic: Urgent Help Needed  (Read 1290 times)

Offline yasser37

  • SF Citizen
  • ***
  • Posts: 228
  • Reputation: 2832
Urgent Help Needed
« on: March 15, 2011, 02:04:12 pm »
Hi ppl

I need urgent help.. I have an exam in two days but I can't seem to solve differential equations correctly

can someone please do June 10 paper 32 Question 7?

Thanks
Logged

elemis

  • Guest
Re: Urgent Help Needed
« Reply #1 on: March 15, 2011, 02:34:10 pm »
Hang on.
Logged

elemis

  • Guest
Re: Urgent Help Needed
« Reply #2 on: March 15, 2011, 02:42:19 pm »
\frac{\mathrm{dx} }{\mathrm{d} t} = \frac{cos^2x}{e^{2t}}

Separating the variables

\int \frac{1}{cos^2x}dx=\int e^{-2t}~dt


\int sec^2x~dx=\int e^{-2t}~dt

<br />tanx=-\frac{1}{2}e^{-2t} +C


When x = 0 t= 0. Input these values into the below equation and find the value of C

tanx=-\frac{1}{2}e^{-2t} +C

C = 0.5

Hence,

tanx=-\frac{1}{2}e^{-2t} + \frac{1}{2}<br /><br />x = tan^{-1}(-\frac{1}{2}e^{-2t} + \frac{1}{2})
« Last Edit: March 15, 2011, 02:47:36 pm by Ari Ben Canaan »
Logged

elemis

  • Guest
Re: Urgent Help Needed
« Reply #3 on: March 15, 2011, 02:46:10 pm »
Did you understand ?
Logged

Offline yasser37

  • SF Citizen
  • ***
  • Posts: 228
  • Reputation: 2832
Re: Urgent Help Needed
« Reply #4 on: March 15, 2011, 06:40:55 pm »
Thanks a lot mate

yes I got it

if possible question 8 in November 08 and November 09 p31 question 10 part 1 
Logged

Offline yasser37

  • SF Citizen
  • ***
  • Posts: 228
  • Reputation: 2832
Re: Urgent Help Needed
« Reply #5 on: March 16, 2011, 05:30:46 am »
anyone?
 :-[

 question 8 in November 08 and November 09 p31 question 10 part 1
Logged

elemis

  • Guest
Re: Urgent Help Needed
« Reply #6 on: March 16, 2011, 02:14:25 pm »
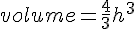
volume~=\frac{4}{3}h^3

Differentiating :

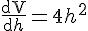
\frac{\mathrm{dV} }{\mathrm{d} h}=4h^2

The rate of change of volume with respect to time is equal to the water input minus the water loss :

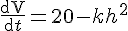
\frac{\mathrm{dV} }{\mathrm{d} t}=20-kh^2

-kh2 represents the loss via leakage

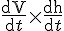
\frac{\mathrm{dV} }{\mathrm{d} t}\times \frac{\mathrm{dh} }{\mathrm{d} t}

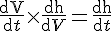
\frac{\mathrm{dV} }{\mathrm{d} t}\times \frac{\mathrm{dh} }{\mathrm{d} V} = \frac{\mathrm{dh} }{\mathrm{d} t}<br />

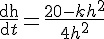
\frac{\mathrm{dh} }{\mathrm{d} t}=\frac{20-kh^2}{4h^2}

Simplify to :

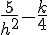
\frac{5}{h^2}-\frac{k}{4}

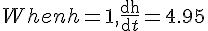
When~h=1,\frac{\mathrm{dh} }{\mathrm{d} t}=4.95

Input h=1 into above equation and find k. You will see the end solution is the equation given in the paper.
Logged
Pages: [1]   Go Up
« previous next »