What about this question, there seems to be two ways of doing it, getting two different solutions. I'm not quite sure whether the 1.5 m is required for the calculation, (maybe for GPE?), or do we use the acceleration formula:
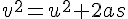
The diagram attached shows a mass of 2.5 kg initially at rest on a rough inclined plane. The mass is now released and acquires a velocity of 4.0ms-1 at P, the base of the incline. Find (a) the work done against friction, (b) the (average) friction force.
I got 20J, 5N, but I did I completely different approach (using GPE) and got dissimilar answers: 17.5J, 4.4N. Which is right - By the way for 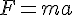 , can we use this formula if we are working out the friction force (ie. the force against the acceleration), or is this only valid for resultant force? I'm confused.
, can we use this formula if we are working out the friction force (ie. the force against the acceleration), or is this only valid for resultant force? I'm confused.
Thanks in advance!
Do you mind if I ask how you got 20J and 5N

The only possible answers am getting are
17.5J and 4.375N.You can use
both methods and I assure you, you'll be getting same answers. I guess you must have done some little mistakes somewhere

I'll elaborate on both methods to help you find your errors :
1. Loss in P.E = Gain in K.E + Work done against friction
mgh = 0.5mv
2 + Work done against friction
Hence Work done against friction = mgh - 0.5mv
2 = 2.5(10)(1.5) - 0.5(2.5)(4)
2 =
17.5JNow you can find the average frictional force = 17.5/4 =
4.375N2. First you need to find the angle of inclination(x) using the distances provided -----> sin x = 1.5/4
Now you need to find the acceleration using
v2 = u2 + 2aS42 = 0 + 2a(4) -----> a =
2m/s
2Using Newton's 2nd law of motion :
Resultant force = ma
mgsin x - Friction = ma
Hence Friction = mgsin x - ma = 2.5(10)(1.5/4) - 2.5(2) =
4.375NNow, Work done against friction = 4.375 x 4 =
17.5JHope it helps
